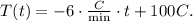We define the following variables and functions:
• t = time,
,
• T(t) = temperature as a function of time.
From the statement, we know that:
• the initial temperature is T(0) = 100°C,
,
• the temperature at time t = 5 minutes is T(5) = 70°C.
If we consider a linear model to describe this problem, we have the general linear equation:
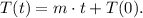
Where m is the rate of change of the temperature. Replacing the data above for t = 5 min, we have:
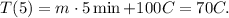
Solving for m, we get:
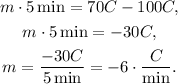
Replacing this value and T(0) = 100°C in the general equation, we get:
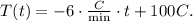
Answer
The equation that model this problem is: