Question

a 6.0cm diameter horizontal pipe gradually narrows to 4.5cm. when water flows through this pipe at a certain rate , the gauge pressure in these two sections is 32.0kPa and 24.0kPa respectively. evaluate the volume flow rate

Answer 1

Q = 0.0077 m³/s

Step-by-step explanation

We have a pipe with two ends that have different diameter:

The given information is,

• d1 = 6 cm

,

• d2 = 4.5 cm

,

• P1 = 32,000 Pa

,

• P2 = 24,000 Pa

By Bernoulli's law - which states that the total presure and kinetic energy throughout the flow is constant. Since this is an horizontal pipe we'll have only two terms in the equation,

`P_1+(1)/(2)\cdot\rho\cdot v^2_1=P_2+(1)/(2)\cdot\rho\cdot v^2_2`

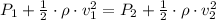
Also, we know that the volume flow rate is also constant,

`Q=A_1\cdot v_1=A_2\cdot v_2`

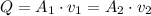
In both equations the speed of the water is missing. Let's solve the second equation for v2,

`v_2=v_1\cdot(A_1)/(A_2)`

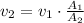
The sectional area of the pipe is a circle, so the equation is,

`A=\pi\cdot(d^2)/(4)`

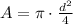
Replace into the equation for v2,

`v_2=v_1\cdot(\pi\cdot(d^2_1)/(4))/(\pi\cdot(d^2_2)/(4))`

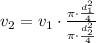
Note that π and 4 get cancelled out because of the fraction,

`v_2=v_1\cdot(d^2_1)/(d^2_2)`

Now replace with the diameters. Because they are in a fraction we can use the diameters in centimeters, and the units cm² get cancelled out,

`v_2=v_1\cdot(6^2)/(4.5^2)`
`v_2=(16)/(9)v_1`

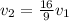
The next step is to replace v2 by this equation into Bernoulli's equation,

`P_1+(1)/(2)\cdot\rho\cdot v^2_1=P_2+(1)/(2)\cdot\rho\cdot((16)/(9)v_1)^2`

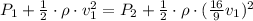
And then solve for v1. First put all the terms containing v1 on the same side of the equation,

`(1)/(2)\cdot\rho\cdot v^2_1-(1)/(2)\cdot\rho\cdot((16)/(9)v_1)^2=P_2-P_1`

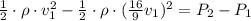
Take out 1/2ρv1² as a common factor,

`(1)/(2)\cdot\rho\cdot v^2_1(1-((16)/(9))^2)=P_2-P_1`

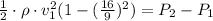
Solve the parenthesis,

`-(175)/(81)\cdot(1)/(2)\cdot\rho\cdot v^2_1=P_2-P_1`

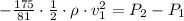
And solve for v1,

`v_1=\sqrt[]{(P_2-P_1)/(-(175)/(81)\cdot(1)/(2)\cdot\rho)}`

Replace P1 and P2. ρ is the density of water, which is about 1000kg/m³.

`v_1=\sqrt[]{(24,000Pa-32,000Pa)/(-(175)/(81)\cdot(1)/(2)\cdot1000(kg)/(m^3))}`

To check the units, remember that Pa = kg/m·s².

`v_1\approx2.72\sqrt[]{\frac{m^3}{m^{}\cdot s^2}}=2.72\sqrt[]{(m^2)/(s^2)}=2.72m/s`

Now, knowing the velocity of the water at one end of the pipe, we can find the volume flow rate,

`Q_{}=A_1\cdot v_1`

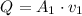
To find the are, now we do have to use the diameter in meters. d1 = 6cm = 0.06m,

`Q=\pi\cdot(0.06^2)/(4)\cdot2.72m/s`
`Q\approx0.0077m^3/s`

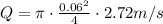
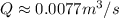
Hence, the volume flow rate is 0.0077 m³/s.