Question

If a wheel starts at an angular velocity of 7.5 rad/s and it comes to rest in 22 seconds, what is the wheel’s angular acceleration? What is the angular displacement of the wheel?

Answer 1

Given:

The initial angular speed is,

`\omega_0=7.5\text{ rad/s}`

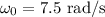
The final angular speed is,

`\omega=0`

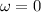
The time taken to stop is,

`t=22\text{ s}`

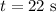
To find:

the wheel’s angular acceleration and the angular displacement of the wheel

Step-by-step explanation:

From kinematics laws for rotational motion, we get,

`\begin{gathered} \omega=\omega_0+\alpha t \\ \end{gathered}`

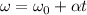
here, the angular acceleration is,

`\begin{gathered} \alpha=(\omega-\omega_0)/(t) \\ =(0-7.5)/(22) \\ =-0.34\text{ rad/s}^2 \end{gathered}`

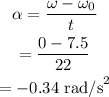
Now,

`\begin{gathered} \omega^2-\omega_0^2=2\alpha\theta \\ \theta=(\omega^2-\omega_0^2)/(2\alpha) \end{gathered}`

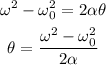
The angular displacement is,

`\begin{gathered} \theta=(0^2-7.5^2)/(2*(-0.34)) \\ \theta=82.7\text{ rad} \end{gathered}`

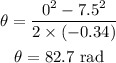
Hence, the angular acceleration is

`-3.4\text{ rad/s}^2`

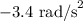
The angular displacement is 82.7 rad.