Solution:
Give the following below
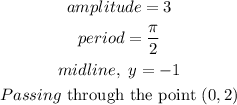
To find the cosine function, we will apply the general formula for cosine function below

To find the value of b
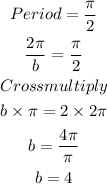
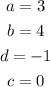
Substitute the values of the variables into the general formula for cosine function
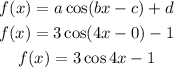
Applying a graphing tool,
The graph of one cycle of the function is shown below