We will have the following:
First, we recall that velocity times time is distance, so the following is true:
*Downstream:
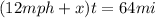
*Upstream:
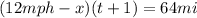
Now, we solve for "t" in both:
**Downstream:
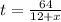
**Upstream:
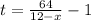
Now, we equal both expressions and solve for "x", that is:
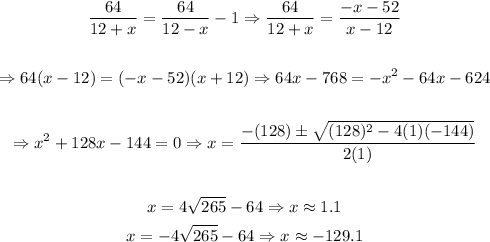
Now, since a negative value for the expressions written won't make much sense [Due to the formulation of the problem], we will have that the speed of the current is approximately 1.1 mph.