Question

If the rate of inflation is 1.9% per year, the future price p(t) (in dollars) of a certain item can be modeled by the following exponential function, where is the number of years from today.Find the price of the item 4 years from today and 10 years from today. p(t) = 1500 * (1.019) ^ t Round your answers to the nearest dollar as necessary.

Answer 1

.Explanation

We are told to find the price of the item 4 years from today and 10 years from today

To do so, we will use the model equation given to us

`P(t)=1500(1.019)^t`

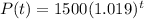
In the first case, the price for 4 years will be when t = 4

So we will have

`\begin{gathered} P(4)=1500(1.019)^4 \\ P(4)=1500*1.07819 \\ P(4)=1617.29 \end{gathered}`

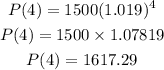
So the price 4 years from today will be $1617

In the second case, we will have to calculate the price for 10 years

So we will have

`\begin{gathered} P(10)=1500(1.019)^(10) \\ P(10)=1500*1207096 \\ P(10)=1810.64 \end{gathered}`

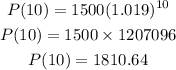
The price 10 years from today will be $1810