Question

All changes savedFor the three-part question that follows, provide your answer to each question in the given workspace.Identify each part with a coordinating response. Be sure to clearly label each part of your response asPart A, Part B, and Part C.A bag contains three blue marbles, five red marbles, and four green marbles.Part A: What is the probability of selecting a red marble?Part B: What is the probability of selecting three red marbles without replacement?Part C: In a short paragraph, explain in your own words your work to Step B.

Answer 1

Part A.

If there are three blue marbles, five red marbles, and four green marbles, the probability of selecting a red marble is

`P=(5)/(3+5+4)=(5)/(12)_{}`

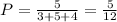
Remember that the probability is the ratio between the number of events and the total number of all the events. In this case, the number of events is 5 because there are 5 red marbles, and the total number of all events is the sum of all the marbles.

Therefore, the probability of selecting red marbles is 5/12.

Part B.

`P=(5)/(12)\cdot(4)/(11)\cdot(3)/(10)=(5\cdot4\cdot3)/(12\cdot11\cdot10)=(60)/(1320)=(30)/(66)=(15)/(33)`

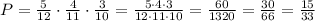
Notice that we have three different ratios, that is because each time we select a red marble it represents a different situation since we won't place back the red marble into the bag, that's why each event decreases by one and each denominator too.

Therefore, the probability of selecting three red marbles without replacement is 15/33.

Part C.

As we said before, in Part B, we had to multiply each probability for each time we select a red marble. It's important to notice that the numerators decreased by 1 (5,4,3) because each time we select a marble we won't place it back, that's the reason why the denominator also decreased by 1.