5, 12, 13
1) Let's sketch this out:
Note that we admit "rise" as the vertical leg, and "run" as the horizontal leg.
2) So we can apply the Pythagorean Theorem. Note that the hypotenuse will be placed on the left:
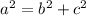
So we can plug into that the given data:
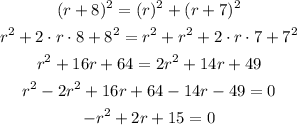
Note that we expand those binomials accordingly to the rule.
Now let's calculate the value of "r":
![\begin{gathered} -r^2+2r+15=0 \\ r^2-2r-15=0 \\ r=\frac{2\pm\sqrt[]{(-2)^2-4(1)(-15)}}{2(1)} \\ r_1=-3 \\ r_2=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6aataoosfl78cjoqohxt4eb1est5ttecko.png)
3) Note that the negative value of r, -3 does not interest us since there are no negative lengths. That's why we are going to consider the positive one: r=5
So the sides are:
r= 5
r+8= 13
r+7 = 12