Answer:
8.81
Explanation:
The standard deviation for a sample is calculated using the formula:
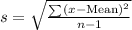
First, find the mean of the data set.
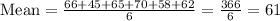
Next, we find the square of the mean deviations for each x.
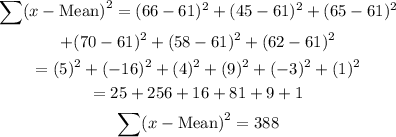
Therefore, the standard deviation of this sample of numbers will be:
![s=\sqrt[]{\frac{\sum^{}_{}(x-\text{Mean)}^2}{n-1}}=\sqrt[]{(388)/(6-1)}=\sqrt[]{(388)/(5)}=8.81](https://img.qammunity.org/2023/formulas/mathematics/high-school/a094pnpiqgsu0xvusje41de62t4g4xec1k.png)
The standard deviation is 8.81 (correct to 2 decimal places).