Question

The area (in square inches) of a rectangle is given by the polynomial function A(b) = b2 + 5b + 6. If the width of therectangle is (b + 3) inches, what is the length?

Answer 1

The area of a rectangle is calculated using the formula:

`area=length* width`

Hence, the width is calculated to be:

`length=(area)/(width)`

The rectangle in the question provides the following information:

`\begin{gathered} area=b^2+5b+6 \\ width=b+3 \end{gathered}`

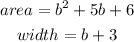
We can solve the division as shown below:

`length=(b^2+5b+6)/(b+3)`

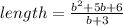
Step 1: Divide the leading term of the dividend by the leading term of the divisor. Write down the calculated result in the upper part of the table. Multiply it by the divisor and subtract the dividend from the obtained result

`\begin{gathered} (b^2)/(b)=b \\ b(b+3)=b^2+3b \end{gathered}`

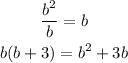
Step 2: Divide the leading term of the dividend by the leading term of the divisor. Write down the calculated result in the upper part of the table. Multiply it by the divisor and subtract the dividend from the obtained result

`\begin{gathered} (2b)/(b)=2 \\ 2(b+3)=2b+6 \end{gathered}`

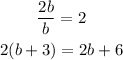
ANSWER

The division yields:

`(b^2+5b+6)/(b+3)=b+2`

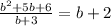
The width is (b + 2) inches.