Question

Right now Jack's age is 4 years more than twice Fred's age. After 8 years, the sum of their ages is 59. FindFred's age.

Answer 1

Jack's age will be represented as "x" and Fred's age will be represented as "y".

We know that right now Jack's age is 4 years more than twice Fred's age, this means:

`x=2\cdot y+4`

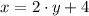
After 8 years the age of each of them must be added by 8 and they will be equal to 59 when added. We have:

`\begin{gathered} (x+8)+(y+8)=59 \\ x+y+16=59 \\ x+y=59-16 \\ x+y=43 \end{gathered}`

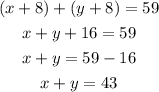
We then have two equations and two variables, therefore we can create a solvable system of equations.

`\mleft\{\begin{aligned}x=2y+4 \\ x+y=43\end{aligned}\mright.`

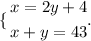
To solve the system o equations we can use the additive method. This is done by multiplying the first equation by "-1" and adding both equations. we have:

`\begin{gathered} \mleft\{\begin{aligned}-x=-2y-4 \\ x+y=43\end{aligned}\mright. \\ -x+x+y=-2y-4+43 \\ y=-2y+39 \\ y+2y=39 \\ 3y=39 \\ y=(39)/(3) \\ y=13 \end{gathered}`

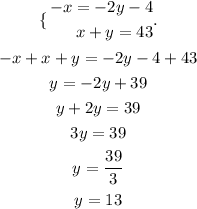
Since the sum of their age must be 43, we have:

`\begin{gathered} x+y=43 \\ x+13=43 \\ x=43-13 \\ x=30 \end{gathered}`

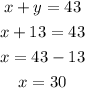
The ages of Jack and Fred are respectively 13 and 30.