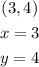Question

Solve the system of equations by graphing. y=1/3x+33x-y=5

Answer 1

The solution to the system of equations is the point at which the two lines meet:

`\begin{gathered} (3,4) \\ x=3 \\ y=4 \end{gathered}`

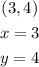
Step-by-step explanation:

Given the system of equation;

`\begin{gathered} y=(1)/(3)x+3\text{ ---1} \\ 3x-y=5\text{ ---2} \end{gathered}`

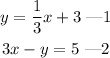
rewrite equation 2 in slope intercept form;

`\begin{gathered} 3x-y=5 \\ y=3x-5\text{ ----2a} \end{gathered}`

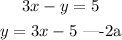
Let us derive two cordinate points for each equation;

`\begin{gathered} y=(1)/(3)x+3\text{ ---1} \\ at\text{ x=0;} \\ y=(1)/(3)(0)+3 \\ y=3 \\ (0,3) \\ at\text{ x=3;} \\ y=(1)/(3)(3)+3 \\ y=1+3 \\ y=4 \\ (3,4) \end{gathered}`
`\begin{gathered} y=3x-5\text{ ----2a} \\ at\text{ x=0;} \\ y=3(0)-5 \\ y=-5 \\ (0,-5) \\ \text{at x=3;} \\ y=3(3)-5 \\ y=9-5 \\ y=4 \\ (3,4) \end{gathered}`

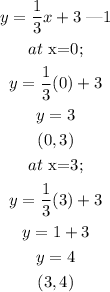
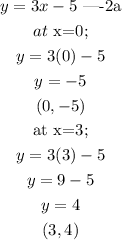
Plotting the coordinate points on the graph we have;

Graphing the two equations, the solution to the system of equations is the point at which the two lines meet.

`\begin{gathered} (3,4) \\ x=3 \\ y=4 \end{gathered}`