Solution
- The formula given is
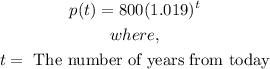
Price for today:
- The number of years from today is 0 years. Implying that

- Thus, we can find the price for today as follows:
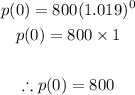
- The cost today is 800
Price 9 years from today:
- The number of years from today is 9 years. Implying that

- Thus, we can find the price 9 years from now as follows:

- The cost 9 years from now is 947.67