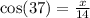Question

14 Choose the correct ratio. 37 sin (37) = 1 tan(37) 14 - sin(37) 14 cos(37) = 2

Answer 1

Notice that the lengths of the side adjacent to the angle of 37° and the hypotenuse are given. Recalling the definitions of the trigonometric functions of an angle in a right triangle:

`\begin{gathered} \sin (\theta)=\frac{\text{Side opposite to }\theta}{\text{Hypotenuse}} \\ \cos (\theta)=\frac{\text{Side adjacent to }\theta}{\text{Hypotenuse}} \\ \tan (\theta)=\frac{\text{Side opposite to }\theta}{\text{Side adjacent to }\theta} \end{gathered}`

We have enough information to find the cosine of the angle of 37°. Then, the correct ratio is:

`\cos (37)=(x)/(14)`