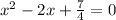Question

Find a quadratic equation in standard form given its roots are:

Answer 1

Given the roots of a quadratic equation:

`(2\pm i√(3))/(2)`

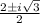
Let's find the equation in standard form.

Apply the standard form of a quadratic equation:

`ax^2+bx+c=0`

Now, we have:

`(x-(2+i√(3))/(2))(x-(2-i√(3))/(2))=0`

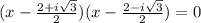
Now, let's expand the equation.

We have:

`\begin{gathered} x(x-(2-i√(3))/(2))-(2+i√(3))/(2)(x-(2-i√(3))/(2))=0 \\ \\ (x^2*2-x(2-i√(3))-x(2-i√(3)))/(2)+(7)/(4)=0 \end{gathered}`

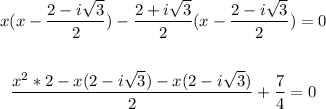
Solving further:

`\begin{gathered} (x(2x-2+√(3)i-(2+√(3)i)))/(2)+(7)/(4)=0 \\ \\ (x(2x-4))/(2)+(7)/(4)=0 \\ \\ x(x-2)+(7)/(4)=0 \\ \\ x^2-2x+(7)/(4)=0 \end{gathered}`

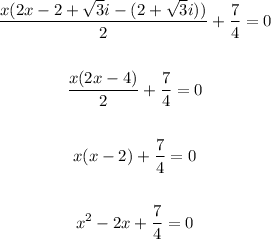
Therefore, the equation in standard form is:

`x^2-2x+(7)/(4)=0`

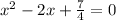
ANSWER:

`x^(2)-2x+(7)/(4)=0`