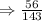Step-by-step explanation:
The number of black balls is
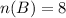
The number of red balls is
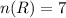
The total number of balls are
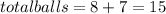
Step 1:
Calculate the numerator
The number of ways to choose 3 black from 8 black balls is given below as
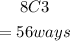
We will then choose the remaining 2 red balls from the 7 red balls below as
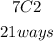
Therefore,
The numerator will be
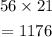
Step 2:
Calculate the denominator
Here we are going to calculate the number of ways to choose 5 balls from a total of 15 balls below as
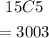
Therefore,
The probability of picking exactly 3 black balls will be
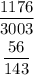
Hence,
The final answer is