Question

Three siblings are comparing the ages. Jenna is the youngest. Her brother Carl is 6 years older than her. Her sister Eva is twice her age. The sum of the ages is 42. Let J represent Jenna’s age. Calculate the ages of the three siblings.

Answer 1

Given the question in the question tab, the following are the solution steps to get the ages of the three siblings.

Step 1: Let us represent the ages of the siblings

Let J represent Jenna's age

Let C represent Carl's age

Let E represent Eva's age

Step 2: Write the statements in a mathematical form

`\begin{gathered} \text{Jenna is the youngest and Carl is 6 years older than her} \\ C=J+6---\text{equation 1} \\ \text{Eva is twice the age of Jenna} \\ E=2J---\text{equation }2 \\ \text{The sum of the ages is 42} \\ C+E+J=42---\text{equation }3 \end{gathered}`

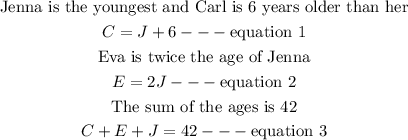
Step 3: We solve for the ages by using the substitution method

`\begin{gathered} \text{Substitute (J+6) for C and 2J for E in equation 3} \\ C+E+J=42\Rightarrow J+6+2J+J=42 \\ \text{Collect like terms} \\ J+2J+J=42-6 \\ 4J=36 \\ J=(36)/(4) \\ J=9 \\ \text{Jenna is 9 years old.} \end{gathered}`

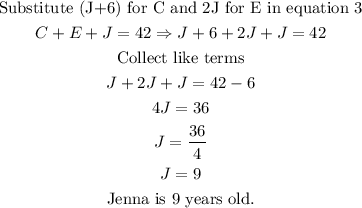
Step 4: Get the age of Carl and Eva using both equat