Question

GH has one endpoint at the origin (0,0). Whichother coordinate would make GH the longestpossible segment?

Answer 1

From the information given, GH is a straight line. One of its endpoints is (0,0).

This means that

x1 = 0, y1 = 0

We want to determine values for x2 and y2 that would give the longest possible length for GH.

The formula for determining the length of a line is expressed as

`\text{length = }√((x2-x1)^2+(y2-y1)^2)`

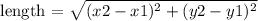
Looking at the above equation, the values of x2 and y2 that would give the longest possible length of GH would be x2 = - 2, y2 = 8

The length of the segment would be

`\begin{gathered} \text{length = }√((-2-0)^2+(8-0)^2) \\ \text{length = }√(68) \end{gathered}`

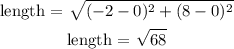
If we input the other option, the length would be lesser than the one we got.

Therefore, the correct option is (- 2, 8)