graph the equation y=x²- 6x - 8. you must plot five points including the roots and the vertex
we have the equation
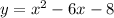
this is a quadratc equation (vertical parabola) open upward (because the leading coefficient is positive)
step 1
Find the vertex
Convert the equation into vertex form
y=a(x-h)^2+k
where
(h,k) is the vertex
Complete the squares
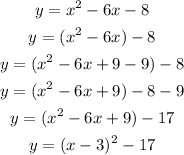
the vertex is the point (3,-17)
step 2
Find the y-intercept
value of y when the value of x is zero
For x=0
y=(0-3)^2-17
y=9-17
y=-8
the y-intercept is (0,-8)
step 3
Find the roots
The roots are the values of x when the value of y is zero
so
For y=0
![\begin{gathered} 0=(x-3)^2-17 \\ (x-3)^2=17 \\ x-3=\pm\sqrt[\square]{17} \\ x=3\pm\sqrt[\square]{17} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wj38psqq8i05q6b34ad8cgfbob7zauv91i.png)
therefore
the roots are
![(3+\sqrt[,]{17},0)](https://img.qammunity.org/2023/formulas/mathematics/college/tgt0tr82z5v4t2h032ax4nvl12l3zhwkct.png)
and
![(3-\sqrt[,]{17},0)](https://img.qammunity.org/2023/formulas/mathematics/college/1i2dytadwo42gcj2xdso2g49png80bkkdy.png)
Simplify
(7.12,0) and (-1.12,0)
step 4
Plot the given points to graph the given function
using a graphing tool
see the attached figure
please wait a minute to plot the points