Question

Hey! I need help solvingThis is from my ACT prep guide

Answer 1

316.1 ft

Step-by-step explanation:

Let's sketch the diagram as seen below;

From the above diagram, we can go ahead and determine the length of the opposite side(x) to angle 56 degrees in the upper triangle as seen below;

`\begin{gathered} \tan 56=(x)/(150) \\ x=150\cdot\tan 56x \\ x=222.4ft \end{gathered}`

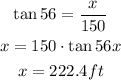
We can also go ahead and determine the length of the opposite side(y) to angle 32 degrees in the lower triangle as seen below;

`\begin{gathered} \tan 32=(y)/(150) \\ y=150\cdot\tan 32 \\ y=93.7ft \end{gathered}`

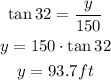
Therefore, the height(h) of the building will be;

`\begin{gathered} h=x+y \\ =222.4+93.7 \\ =316.1ft \end{gathered}`

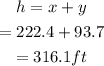
So the neighboring building is 316.1 ft tall.