Question

Two number cubes are rolled. What is the probability:a. That the sum is 7? P(sum 7)b. The product is less than 20? P(Product<20)

Answer 1

`\begin{gathered} a.)(1)/(6) \\ b)(7)/(9) \end{gathered}`

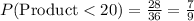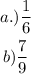
1) We can tackle this question by enlisting all the possible outcomes when two dices are rolled.

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

Notice that we have 36 results altogether.

2) Now let's find the Probabilities.

a) The sum is 7.

Let's bold all the favorable outcomes:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

So we have 6 favorable outcomes. Let's find the Probability of that sum is 7:

`P=(6)/(36)=(1)/(6)`

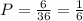
b) Now, let's bold all the possible outcomes whose product is less than 20

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

So, there are 28 favorable outcomes out of 36.

So we can find our Probability of outcomes whose product is less than 20:

`P(\text{Product}<20)=(28)/(36)=(7)/(9)`