Question

Use the factor theorem to find all the real zeros for the given polynominal and one of it’s factors.

Answer 1

Given:

`3x^3+x^2-20x+12`

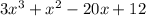
Factor: x+3

To find the zeros:

Using synthetic division,

So, the polynomial can be written as,

`3x^3+x^2-20x+12=(x+3)(3x^2-8x+4)`

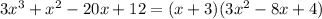
Let us consider,

`p(x)=3x^2-8x+4`

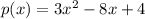
Put x=2, we get

`\begin{gathered} p(2)=3(2^2)-8(2)+4 \\ =12-16+4 \\ =0 \end{gathered}`

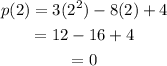
Hence, x=2 is the other one zero of the polynomial.

Put x=2/3, w get

`\begin{gathered} p((2)/(3))=3((2)/(3))^2-8((2)/(3))+4 \\ =(4)/(3)-(16)/(3)+4 \\ =-(12)/(3)+4 \\ =(-12+12)/(3) \\ =0 \end{gathered}`

Hence, x=2/3 is the other one zero of the polynomial.

Hence, the zeros of the polynomial are,

`-3,(2)/(3),\text{ and, 2}`