Question

Target sells sets of pots ($30) and dishes ($20). On July 4 weekend, target’s total sales were $700. People bought a total of 30 sets of pots and dishes. How many of each set did target sell?

Answer 1

Let's call p pots and d dishes.

We know that the sets of pots cost $30 and the set of dished cost $20, we express this as the following

`30p+20d=700`

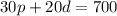
Since the target sales are $700.

The total number of pots and dishes people bought were 30 sets, we express this as the following.

`p+d=30`

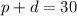
We can form a system of equations we these equations.

`\mleft\{\begin{aligned}30p+20d=700 \\ p+d=30\end{aligned}\mright.`

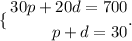
To solve this, we multiply the second equation by -20, then we sum equations to eliminate d and solve for p.

`\begin{gathered} \mleft\{\begin{aligned}30p+20d=700 \\ -20p-20d=-600\end{aligned}\rightarrow10p=100\mright. \\ p=(100)/(10)=10 \end{gathered}`

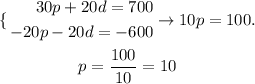
There were sold 10 sets of pots.

Now, we find the sets of dishes sold.

`\begin{gathered} p+d=30 \\ 10+d=30 \\ d=30-10 \\ d=20 \end{gathered}`

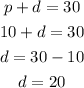
There were sold 20 sets of dishes.