Question

find the 6th term of the geometric sequence with the given term.please I really need help I need to submit that before 10pm

Answer 1

Answer: The 6th term of the geometric progression is 324

Given that :

a2 = 4, and a5 = 108

Firstly, we will need to find the first term and the common ratio of the sequence

`\begin{gathered} \text{The nth term of a geometric progression is written as} \\ a_n=ar^{n\text{ - 1}} \\ \text{Where a = first term, r = common ratio and n = number of terms} \\ a_{2\text{ }}=\text{ 4, and }a_5\text{ = 108} \\ 4=ar^{2\text{ - 1}} \\ 4=ar^1\text{ ------ equation 1} \\ 108=ar^{5\text{ - 1}} \\ 108=ar^4\text{ -------- equation 2} \\ \text{Divide equation 2 by 1} \\ (108)/(4)\text{ = }(ar^4)/(ar^1) \\ a\text{ is common in both denominator and numerator} \\ 27\text{ = }(r^4)/(r1) \\ 27=r^{4\text{ - 1}} \\ 27=r^3 \\ \text{Take the cube roots of both sides} \\ \sqrt[3]{27}\text{ = }\sqrt[3]{r^3} \\ r\text{ = }\sqrt[3]{27} \\ r\text{ = 3} \\ To\text{ find a, substitute the value of r into equation 1} \\ 4=ar^1 \\ 4\text{ = a x 3} \\ \text{Divide both sides by 3} \\ a\text{ = }(4)/(3) \end{gathered}`

To find the 6th term, we will substitute the value a and r into the formula

`\begin{gathered} \text{ Since, a}_{n\text{ }}=ar^{n\text{ - 1}} \\ a_{6\text{ }}=\text{ }(4)/(3)^{}\cdot3^{6\text{ - 1}} \\ a_6=\text{ }(4)/(3)\cdot3^5 \\ a_6\text{ = }\frac{4\text{ x 243}}{3} \\ a_6\text{ = }(972)/(3) \\ a_6\text{ = 324} \end{gathered}`

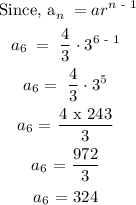
Hence, the 6th term of the geometric progression is 324