9. We have the lines:
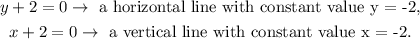
Plotting the lines, we get the following graph:
From the graph, we see that the lines are perpendicular.
11. We have the lines:
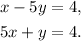
We rewrite the equations of the lines as:
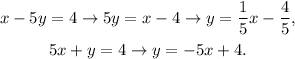
The general equation of a line with slope m and y-intercept b is:
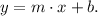
The slopes of the lines are:
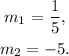
Two lines with slopes m1 and m2 are perpendicular if they satisfy the equation:
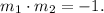
Replacing the values above, we get:
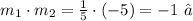
So we conclude that the lines are perpendicular.
Answer
9. Perpendicular
11. Perpendicular