Question

Finding y intercepts and x intercepts of the graph of the function

Answer 1

We have the next function

`f(x)=-2x^3+10x^2+48x`

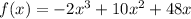
And we must find its x-intercepts and y-intercepts

1. y-intercepts:

To find the y-intercepts we need to replace x = 0 in the function and then solve it for y

So, replacing x = 0 in the function we obtain

`\begin{gathered} y=-2(0)^3+10(0)^2+48(0) \\ y=0+0+0 \\ y=0 \end{gathered}`

That means, the y-intercept of the function is 0.

2. x-intercepts:

To find the y-intercepts we need to replace y = 0 in the function and then solve it for x

So, replacing y = 0 in the function we obtain

`0=-2x^3+10x^2+48x`

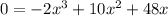
Now, we must solve it for x:

1. we must extract the common factor -2x

`0=-2x(x^2-5x-24)`

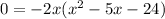
2. we must factor the polynomial inside the parentheses

`0=-2x(x-8)(x+3)`

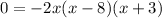
3. We must divide both sides by -2

`0=x(x-8)(x+3)`

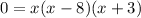
We can see that the values for x that satisfy the equality are 0, 8 and -3

That means, the x-intercepts of the function are 0, 8 and -3.

ANSWER:

y-intercept(s): 0

x-intercept(s): 0, 8, -3