Question

Write the equation in slope-intercept form through the point (4, -4) and is perpendicular to the line y = -4x - 2 and graph.

Answer 1

`y=(1)/(4)x-5`

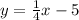
Step-by-step explanation

Step 1

when 2 lines are perpendicular, the product of their slopes is equal to -1

`\begin{gathered} if \\ \text{y}_1\perp y_2 \\ \text{then} \\ slope_1\cdot slope_2=-1 \end{gathered}`

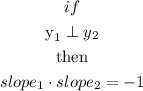
Now, we have

`\begin{gathered} y=-4x-2\Rightarrow y=mx+b \\ \text{Hence} \\ m_1=\text{slope1}=-4 \end{gathered}`

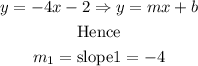
use the equation to find slope2 ( the slope of the line we are looking for)

`\begin{gathered} slope_1\cdot slope_2=-1 \\ -4\cdot m_2=-1 \\ m_2=(-1)/(-4)=(1)/(4) \\ \\ \text{slope}2=(1)/(4) \end{gathered}`

Step 2

find the eq using:

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{Let} \\ m=\text{slope}2=(1)/(4) \\ P(x_1,y_1)=(4,-4) \end{gathered}`

replacing

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-4)=(1)/(4)(x-4) \\ y+4=(1)/(4)x-(4)/(4) \\ y=(1)/(4)x-1-4 \\ y=(1)/(4)x-5 \end{gathered}`

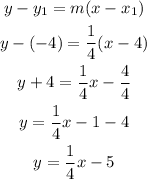
I hope this helps you