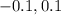z-score
z-score tables usually give the area under the curve of a normal distribution between -∞ and a z-score like the one shaded in blue:
However, we must find the area under the curve between -z and z, something like the red area:
Here it's important to note that the total area under the curve of the normal distribution is equal to one. If the area between -z and z is equivalent to the 8% (i.e. is equal to 0.08) then the sum of the green areas must be the remaining 92% (i.e. 0.92). Now, the curve of the normal distribution is symmetric which implies that both green areas are equal. Then each green area is equivalent to 92/2%=46% of the total area under the curve. Therefore, each area in green is equal to 0.46. What does this mean? It means that if we look for 0.46 in a z-socre table we'll find the value of -z and with it the value of z. So let's find 0.46 in a z-score table:
So 0.46 is located at row -0.1 and column 0.00 which means that its associated with the score -0.1. Then -z=-0.1 and z=0.1. Then the answer is: