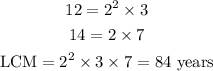Part B
If 12 -year, 14 -year, and 16 -year cicadas that all appear this year, the next time they will all appear together can be determined by finding the lowest common multiple of 12, 14, and 16.
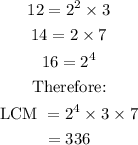
After 336 years, all three types of cicadas will appear together again.
Part C
Stephans method will work for the 13-year and 17-year cicadas since they are prime numbers.
However, it would not work in the case of the 12 -year, 14 -year, and 16 -year cicadas.
Going by Stephan's method, the next time the 12-year and 14-year cicadas will appear together will be:
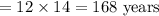
In actual fact, the next time they will appear together is the LCM of 12 and 14.