Question

you can determine equation of a line or the equation of an exponential given any two points. that lies on the curves.in this excerise we will pick two special points.consider the points(0,5) and (1,15) a. write the equation of the exponential that passes between these points in the y=a(b)^form b. sketch the two curves on the axes below .label with their equation

Answer 1

`y=ab^x`

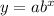
we need to find the value of a and b

The points given are (0, 5) and (1, 15)

For the first point (0, 5)

`5=ab^0`
`5=a`

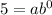
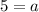
The second point is (1, 15)

substitute the points in the formula

`15=ab^1`

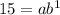
substitute a=5 and solve for b

`15\text{ =5b}`

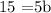
Divide both-side of the equation by 5

`3\text{ = b}`

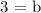
To write our equation, we will simply substitute a=5 and b =3 into the formula

Thus the equation is:

`y=5(3)^x`

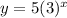
b)Below is the attached graph