In order to calculate P(B|A), that is, the probability of B given A, we can use the following formula:
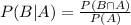
Since the events are independent, we also have the following:
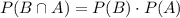
So we have that:
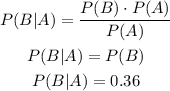
So the probability of B given A is 0.36.
(The probability of B given A being the same probability of B makes sense, since the events are independent, so A happening does not affect B)