Question

What would be the multiple choice anwser to this problem

Answer 1

1st option: The exponential grows at approximately half the rate of the quadratic

Explanation:

We compute the rate change in each case, to determine the proportion, just like this:

`f(x)=(f(b)-f(a))/(b-a)`

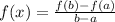
We substitute the values in each case:

`\begin{gathered} \text{ Exponential:} \\ \\ f\mleft(x\mright)=(2-1)/(1-0)=(1)/(1)=1 \\ \\ \text{ Quadratic:} \\ \\ f(x)=(2-0)/(1-0)=(2)/(1)=2 \\ \\ \text{ Therefore, te ratio would be:} \\ \\ r=\frac{\text{ Exponential}}{\text{Quadratic}}=(1)/(2) \\ \\ \end{gathered}`

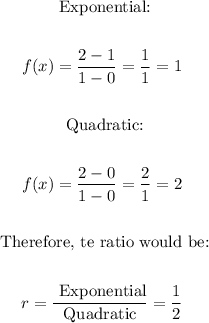
Therefore, the correct answer is 1st option: The exponential grows at approximately half the rate of the quadratic