Step-by-step explanation
We need to apply the exponencial decay in order to get the final elevation of the mountain:
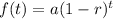
Where a is the initial value, a=1,283 meters and r is the rate in decimal form r= 5/100 = 0.05 and t = time = 2 millenials
Then, we need to substitute the terms:
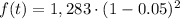
Subtracting numbers:
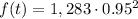
Computing the power:
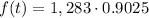
Multiplying numbers:
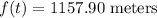
Rounding to the nearest whole number:
Final Elevation = 1158 meters