Question

Help with number 2 finding the transition rule and both coordinate points/image

Answer 1

Given:

In the triangle PQR, the vertices are P(2,1), Q(4,1), and R(4, -3).

To find the vertices over 90 degrees rotation about the origin:

As we know,

To rotate the figure 90 degrees clockwise about a point, every point (x, y) will rotate to (y, -x).

That is, the transformation rule is,

`(x,y)\Rightarrow(y,-x)`

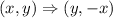
After 90 degrees clockwise rotation about the origin, the triangle PQR becomes P'Q'R'.

Thus,

The points of the triangle P'Q'R' are, P'(1, -2), Q(1, -4), and R(-3, -4).