Question

20 *K-150-U22-1+1=2 min Identify the vertex, axis of symmetry, and min/max value of each. 11) f(-2,2 54 +241 12) f(0) - 181 +86 Sadaxant Morry) (lju

Answer 1

`f(x)=-x^2-10x-30`

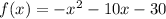
we will find relevant points for example

y-intercept

when the value of x=0

`\begin{gathered} y=-(0)^2-10(0)-30 \\ y=-30 \end{gathered}`

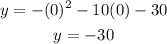
we have a point

`(0,-30)`

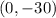
x-Intercept

when the value of f(x)=0

`\begin{gathered} 0=-x^2-10x-30 \\ -x^2-10x-30=0 \\ x^2+10x+30=0 \end{gathered}`

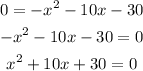
to solve x we use the quadratic formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a is 1, b is 10 and c 30

replacing

`\begin{gathered} x=\frac{-(10)\pm\sqrt[]{(10)^2-4(1)(30)}}{2(1)} \\ \\ x=\frac{-10\pm\sqrt[]{100-120}}{2} \\ \\ x=\frac{-1\pm\sqrt[]{-20}}{2} \end{gathered}`

values of x-intercept will be imaginary(becuse a negative number into a root have imaginary solutions), then we can graph on this plane

then we ignore these values

Vertex

we can find the vertex point using

`x=(-b)/(2a)`

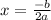
where a is -1, and b -10

then replacing

`\begin{gathered} x=(-(-10))/(2(-1)) \\ \\ x=-(10)/(2)=-5 \end{gathered}`

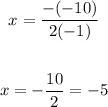
replace x on function

`\begin{gathered} y=-(-5)^2-10(-5)-30 \\ y=-25+50-30 \\ y=-5 \end{gathered}`

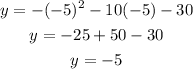
then vertex point is

`(-5,-5)`

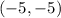
Finally

using vertex point and y-intercept we can graph

We know it is a parable because degree of polynomial (grater exponent) is 2

the parable opens down because the sign of the first term is negative

then place the points and apply the previous tips