Question

What is the least common multiple of 24 and 60?

Answer 1

To find the least common multiple of 24 and 60, factor each number in terms of its prime factors.

24

24 is divisible by 2. Since 24/2 = 12, then:

`24=2\cdot12`

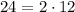
12 is divisible by 2. Since 12/2 = 6, then:

`24=2\cdot2\cdot6`

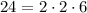
6 is divisible by 2. Since 6/2 = 3, then:

`24=2\cdot2\cdot2\cdot3`

3 is a prime number. Therefore, the prime factorization of 24 is:

`24=2^3\cdot3`

60

From a similar procedure, we can see that:

`\begin{gathered} 60=2\cdot30 \\ =2\cdot2\cdot15 \\ =2\cdot2\cdot3\cdot5 \\ \therefore60=2^2\cdot3\cdot5 \end{gathered}`

Once we know the prime factorization of 24 and 60, the least common multiple of 24 and 60 can be found multiplying the greatest power of each prime number that appears in the prime factorizations.

For the prime number 2, notice that the greatest power is 2^3.

For the prime number 3, the greatest power is 3^1.

For the prime number 5, the greatest power is 5^1.

Then, the least common multiple will be:

`2^3\cdot3\cdot5=8\cdot3\cdot5=120`

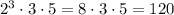
This means that 120 is the lowest number that can be divided by 24 and by 60.