Question

Belief in UFOs A survey found that 5% of people believe that they have seen a UFO. Choose a sample of 12 people at random.Find the probability of the following. Round intermediate calculations and final answers to at least three decimal places.(a) At least 3 people believe that they have seen a UFOp (at least 3 people believe that they have seen a UFO) =(B) 3 or 4 people believe that they have seen a UFO p (at least 3 or 4 people believe that they have seen a UFO) =(C) exactly 2 people believe they have seen a UFOP (exactly 2 people believe they have seen a UFO) =

Answer 1

The given information is:

- p=0.05 (the probability of success)

- n=12 (the sample size)

We can apply the binomial distribution formula to find the probabilities. The formula is:

`P(x)=(n!)/((n-x)!x!)p^xq^(n-x)`

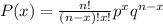
q is equal to 1-p, so:

`q=1-0.05=0.95`

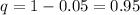
a. Find the probability that at least 3 people believe that they have seen a UFO:

This is equal to:

`P(x\ge3)=1-(P(x=0)+P(x=1)+P(x=2))`

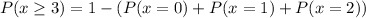
Let's find the individual probabilities:

`\begin{gathered} P(x=0)=(12!)/((12-0)!1!)*0.05^00.95^(12-0) \\ P(x=0)=1*1*0.5404 \\ P(x=0)=0.5404 \\ \\ P(x=1)=(12!)/((12-1)!1!)*0.05^10.95^(12-1) \\ P(x=1)=12*0.05*0.5688 \\ P(x=1)=0.341 \\ \\ P(x=2)=(12!)/((12-2)!2!)*0.05^20.95^(12-2) \\ P(x=2)=66*0.0025*0.5987 \\ P(x=2)=0.099 \end{gathered}`

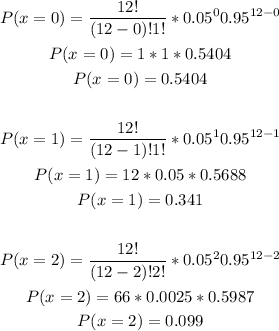
So, the P(x>=3) is:

`\begin{gathered} P(x\ge3)=1-(0.5404+0.341+0.099) \\ P(x\ge3)=0.0196 \end{gathered}`

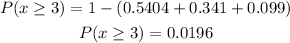
The probability that at least 3 people believe that they have seen a UFO is 0.0196.

b. P(3 or 4 people believe that they have seen a UFO):

This is given by:

`P(3\leq x\leq4)=P(x=3)+P(x=4)`

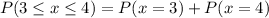
Let's find the individual probabilities:

`\begin{gathered} P(x=3)=(12!)/((12-3)!3!)*0.05^30.95^(12-3) \\ P(x=3)=220*0.0001*0.6303 \\ P(x=3)=0.0173 \\ \\ P(x=4)=(12!)/((12-4)!4!)*0.05^40.95^(12-4) \\ P(x=4)=495*0.000006*0.663 \\ P(x=4)=0.0021 \\ \\ \text{ So:} \\ P(3\leq x\leq4)=0.0173+0.0021=0.0194 \end{gathered}`

The probability that 3 or 4 people believe that they have seen a UFO is 0.0194.

c. P(exactly 2 people believe they have seen a UFO)

This is equal to:

`\begin{gathered} P(x=2) \\ \text{ We already found it in part A, so:} \\ P(x=2)=0.099 \end{gathered}`

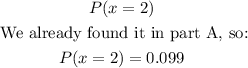
The probability that exactly 2 people believe they have seen a UFO is 0.099.