The following function gives the height of an object thrown straight up after t seconds:
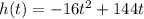
It's required to find h(2) and h(5).
a) To find h(2), substitute the value t = 2 into the equation as follows:
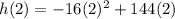
Operating:
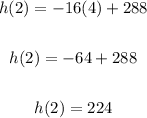
b) Now find h(5):
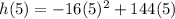
Calculating:
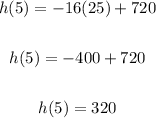
The required heights are:
h(2) = 224
h(5) = 320