We are told that the cost of making 14 tables is 1210 and that the cost of making 26 tables is 1750. If this is a linear relationship, this means that we want to find a line of the form

where m is the slope and b is the y-intercept that passes through the given points.
In our case we are given the points (14,1210) and (26,1750). We will calcualte the slope m as follows: given poitns (a,b) and (c,d) the slope is given by the formula
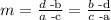
In our case we have a=14, b=1210, c=26 and d=1750. So
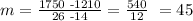
Note that this slope reprents the cost per table. So the cost per table is 45.
Now we want to find the value of b. So far the equation looks like this
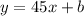
from this formula, we want that when x=14, then y=1210. So we get the equation

So if we subtract 630 on both sides, we get that
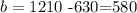
So the linear equation is
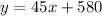
this means that the cost of 24 tables is obtained by replacing the value of x by 24. So we get
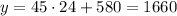
So the cost for 24 tables is 1660