Question

If y varies directly with x, and x = 12 when y = 5, what is the value of x when y = 12?A 284B 25C 27D 26.6

Answer 1

If y varies directly with x, we can write the following relationship:

`y=kx`

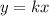
where k is the constant of proportionallity. Now, when x=12, y is 5, then we get

`5=k\cdot12`

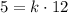
then, k is equal to

`k=(5)/(12)`

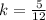
So, our relation is

`y=(5)/(12)x`

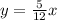
In order to find x, we must substitute y=12 in this last expression, that is,

`12=(5)/(12)x`

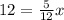
By moving 12 to the left hand side, we get

`\begin{gathered} 12*12=5x \\ 144=5x \\ x=(144)/(5) \\ x=28.8 \end{gathered}`

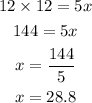
then the answer is 28.8 which can be written as

`28(4)/(5)`

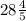
which corresponds to option a.