Given:
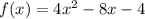
The x-intercepts are the values of x where the function or y-coordinate is zero.
Therefore, the x - intercepts are given when f(x)=0
Hence putting f(x)=0,we get:
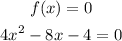
The solutions of quadratic equation are given as:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Here, a = 4 b = -8 c = -4,
![\begin{gathered} x=\frac{8\pm\sqrt[]{64-(4*-4*4)}}{2*4} \\ =\frac{8\pm\sqrt[]{64+64}}{8} \\ =\frac{8\pm\sqrt[]{128}}{8} \\ =\frac{8+\sqrt[]{128}}{8},\frac{8-\sqrt[]{128}}{8} \\ =(8+11.3137)/(8),(8-11.3137)/(8) \\ =(19.3137)/(8),(-3.3137)/(8) \\ =2.4142125,-0.4142125 \\ =2.4,-0.4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ocuhof7knum8rxj4ri1j5ttyw0s3mrni5f.png)
Hence, the x intercepts are ( - 0.4,0 ) and ( 2.4,0)
Since the graph is an upward parabola, it will have a minimum value at its vertex that is (1,-8) and hence, the minimum value of f(x) is - 8.