Question

Solve the following radical equation: √(x2 - 12x + 44) = 3.

Answer 1

Step-by-step explanation

We must solve the following equation for x:

`√(x^2-12x+44)=3`

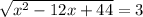
We can square both sides of the equation:

`\begin{gathered} (√(x^2-12x+44))^2=3^2 \\ x^2-12x+44=9 \end{gathered}`

Then we substract 9 from both sides:

`\begin{gathered} x^2-12x+44-9=9-9 \\ x^2-12x+35=0 \end{gathered}`

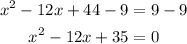
Now we have a quadratic expression equalized to 0. The solutions to this equation are given by the quadratic solving formula. For an equation ax²+bx+c=0 the quadratic formula states that its solutions are:

`x=(-b\pm√(b^2-4ac))/(2a)`

For the equation we found before we have a=1, b=-12 and c=35. Then its solutions are:

`\begin{gathered} x=(-(-12)\pm√((-12)^2-4*1*35))/(2*1)=(12\pm√(144-140))/(2)=(12\pm√(4))/(2) \\ x=(12\pm2)/(2) \end{gathered}`

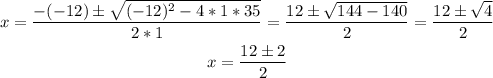
So there are two solutions:

`\begin{gathered} x=(12+2)/(2)=(14)/(2)=7 \\ x=(12-2)/(2)=(10)/(2)=5 \end{gathered}`Answer

Then the answers are x=5 and x=7.