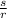Question

For #1 - 4, use the given diagrams and what you have learned about similar polygons. Hint: use the radius of the circles.I already did #1, so can you answer #2 and or all of the other ones if you have the time?

Answer 1

From the given figure we can find the radii of the 3 circles

For circle A:

The center of the circle is (1, 5), and the circle touches the x-axis at the point (0, 0)

Then the radius of the circle is the difference between their y-coordinates

`\begin{gathered} r_A=5-0 \\ r_A=5 \end{gathered}`

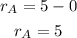
For circle B:

The center of the circle is (-4, -4) and the circle passes through the point (-4, -1), then the radius of the circle is

`\begin{gathered} r_B=-1--4 \\ r_B=-1+4 \\ r_B=3 \end{gathered}`

For circle C:

The center of the circle is (6, -7) and the circle passes through the point (6, -3), then the radius of the circle is

`\begin{gathered} r_C=-3--7 \\ r_C=-3+7 \\ r_C=4 \end{gathered}`

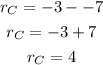
Now we can answer the question

1. The scale factor of dilation that maps the circle A onto a circle congruent to circle B is

`(3)/(5)`

2. The scale factor of dilation that maps the circle B onto a circle congruent to circle C is

`(4)/(3)`

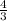
3. The scale factor of dilation that maps the circle C onto a circle congruent to circle A is

`(5)/(4)`

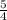
4. From 1, 2, and 3 the scale factor is the ratio between the radius of the new circle to the radius of the old circle, then

The scale factor of dilation of a circle of radius r onto a circle of radius s is

`(s)/(r)`