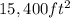Solution:
Given:
A circular field with a radius of 70-foot
To find the area watered by the irrigation system, since the field is circular, we use the area of a circle.
The area of a circle is given by;
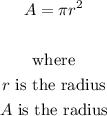
Hence,
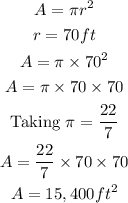
Therefore, the exact area watered by the irrigation system is;