Given:
Area of the trapezoid, A = 9.2 cm^2
Long base, a = 3.2 cm
Short base, b = 2.9 cm
Let's find the height of the trapezoid.
Apply the formula:
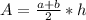
Where h is the height.
Substitute values into the equation:
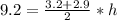
Let's solve for h:
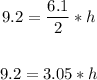
Divide both sides by 3.05:
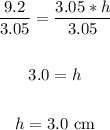
Therefore, the height of the trapezoid is 3.0 cm
ANSWER:
3.0 cm