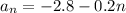Question

I need help with 2 and 3 a through c on both questions

Answer 1

In the arithmetic sequence, the rule is

`a_n=a_{}+(n-1)d`

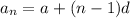
a is the first term and d is the common difference

n is the position of the term

We have the value of the 7th term, then

n = 7, so we can make an equation for it by using the rule above

`\begin{gathered} a_7=a+(7-1)d \\ a_7=a+6d \end{gathered}`

Substitute a7 by its value -4.2, then

`a+6d=-4.2`

We will make the same with a23

n = 23, then

`\begin{gathered} a_(23)=a+(23-1)d \\ a_(23)=a+22d \end{gathered}`

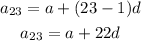
Substitute a23 by its value -7.4

`a+22d=-7.4`

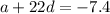
Now we have a system of equations to solve it to find a and d

a + 6d = -4.2 (1)

a + 22d = -7.4 (2)

Subtract (1) from (2)

(a - a) + (22d - 6d) = (-7.4 - -4.2)

0 + 16d = -3.2

16d = -3.2

Divide both sides by 16 to find d

d = -0.2

To find a substitute d in equation (1) by -0.2

a + 6(-0.2) = -4.2

a - 1.2 = -4.2

Add 1.2 to both sides

a = -3

a) the first term is -3

b) the common difference is -0.2

To find the term 67th substitute n by 67

`\begin{gathered} a_(67)=-3+(67-1)(-0.2) \\ a_(67)=-3+66(-0.2) \\ a_(67)=-3+-13.2 \\ a_(67)=-16.2 \end{gathered}`

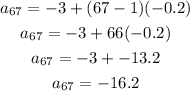
c) the value of the 67th term is -16.2

Let us find the rule of the sequence

`\begin{gathered} a_n=-3+(n-1)(-0.2) \\ a_n=-3+n(-0.2)-1(-0.2) \\ a_n=-3-0.2n+0.2 \\ a_n=-2.8-0.2n \end{gathered}`

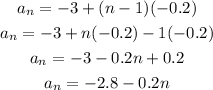
d) The formula of the nth term is

`a_n=-2.8-0.2n`