Question

Please solve this is a not a test or quiz it is a question by my teacher as how to solve the problem

Answer 1

0

Explanation:

Consider the diagram below:

Point P divides segment CD in the ratio 3:2.

To find the coordinate of P, we use the formula for the internal division of a line segment given below:

`P(x,y)=\mleft((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\mright)`

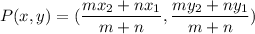
Thus, the x-coordinate of P is:

`\begin{gathered} (mx_2+nx_1)/(m+n)=(3(4)+2(-6))/(3+2)\text{ where }\begin{cases}m\colon n=3\colon2 \\ x_1=-6,x_2=4\end{cases} \\ =(12-12)/(5) \\ =(0)/(5) \\ =0 \end{gathered}`

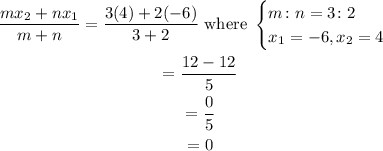
The x-coordinate of P is 0.

Extra

The y-coordinate of P is:

`\begin{gathered} \frac{my_2_{}+ny_1}{m+n}=(3(5)+2(0))/(3+2)\text{ where }\begin{cases}m\colon n=3\colon2 \\ y_1=0,y_2=5\end{cases} \\ =(15+0)/(5) \\ =(15)/(5) \\ =3 \end{gathered}`

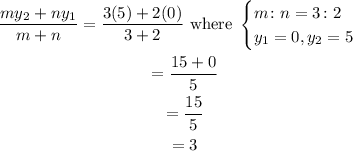
The y-coordinate of P is 3.