41.13
Step-by-step explanation
Step 1
find the volume of the cylinder, the volume of a cylinder is given by:

Let
diameter=8
heigth=13
then
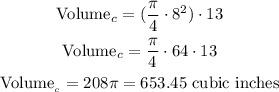
Step 2
find the volume of the rectangular prism, the volume is given by:
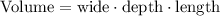
Let
wide=32 in
depth=21 in
length=40 in
then

Step 3
finally, compare the volumes to figure out number of cylinder container of water near to completely fill the

it means you need 41.13 cilynders to fill the container.
I hope this helps you