Question

How far above the ground is the dog's paw? Express your answer to the nearest inch.XPythagorean TheoremEdit my response

Answer 1

25 inches

Step-by-step explanation

the dog's paw forms a rigth triangle, so we can use Pythagoras theorem

wich

`a^2+b^2=c^2`

let

a=a

b=26

c=36

replace

`a^2+26^2=36^2`

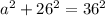
Step 2

solve for x

In an equation, the additive property of equality states that if we add or subtract the same number to both sides of an equation, the sides remain equal. This property holds true for whole numbers as well.

Hence

subtract square 26 in both sides

`\begin{gathered} a^2+26^2=36^2 \\ a^2+26^2-26^2=36^2-26^2 \\ a^2=36^2-26^2 \\ a^2=620 \end{gathered}`

Step 3

finally, The squaring property of equality states that when A = B then A2 = B2. We can use the squaring property of equality when solving equations with square roots.

so

`\begin{gathered} a^2=620 \\ \sqrt[]{a^2}=\sqrt[]{620} \\ a=24.89 \\ \text{rounded to the nearest inch} \\ a=25 \end{gathered}`

I hope this helps you