Question

Experiment 3, you need to prepare a 30 mL solution of a 1:6 syrup solution.You have on hand a 50% syrup solution, and a 1:200 soda solution.How many mLs of soda solution do you need to create this final solution?How many mLs of syrup solution do you need to create this final solution?

Answer 1

Given:

Total solution = 30 ml

The final solution ratio is 1 part syrup to 6 parts soda.

50% syrup solution.

1:200 soda solution.

Find-: How many soda solutions need to create the final sol.

Sol:

Let x = Number of liter of the 50% syrup solution.

y = Number of a liter of the 1 parts syrup to 200 parts soda solution.

So,

`x+y=30`

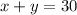
1:200 soda solution and 50% syrup.

`(1)/(2)x+(1)/(201)y=(1)/(7)*30`

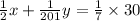
Solve for "x" and "y" the put

`y=30-x`
`\begin{gathered} (1)/(2)x+(1)/(201)(30-x)=(1)/(7)*30 \\ \\ x=8.356 \end{gathered}`

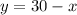
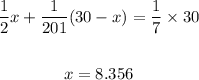
Then the value of "y" is:

`\begin{gathered} y=30-x \\ \\ y=21.644 \end{gathered}`

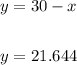
Final sol. will be 30 ml total,

It will contain 8.356 ml of 50% syrup solution.

it will contain 21.644 ml of 1 part syrup to 200 parts soda solution

For the total amount of syrup in the final solution.

`\begin{gathered} (1)/(2)(8.356)+(1)/(201)(21.644) \\ \\ =4.286 \end{gathered}`

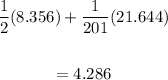
4.286 ml of pure syrup